We’ll continue the plan to rate movies with Markov chains.
This time we’ll learn a Markov chain from movie plots.

Previous blog post
all posts about Markov chains
code

Model

We’ll use this model

  case class Link(to: Token, count: Int)
  case class Links(links: List[Link])
  case class MarkovChain(map: Map[Token, Links])

If we learn a chain from the sentence The cat sits on the mat, it should look like this:

MarkovChain(
        Map(
          StartToken -> Links(List(Link(WordToken("the"), 1))),
          WordToken("the") -> Links(List(Link(WordToken("cat"), 1), Link(WordToken("mat"), 1))),
          WordToken("cat") -> Links(List(Link(WordToken("sits"), 1))),
          WordToken("sits") -> Links(List(Link(WordToken("on"), 1))),
          WordToken("on") -> Links(List(Link(WordToken("the"), 1))),
          WordToken("mat") -> Links(List(Link(EndToken, 1)))
        )
      )

The probability to go from the to cat is 0.5, because we’ve seen the cat occur once, divided by the 2 times that we’ve seen the

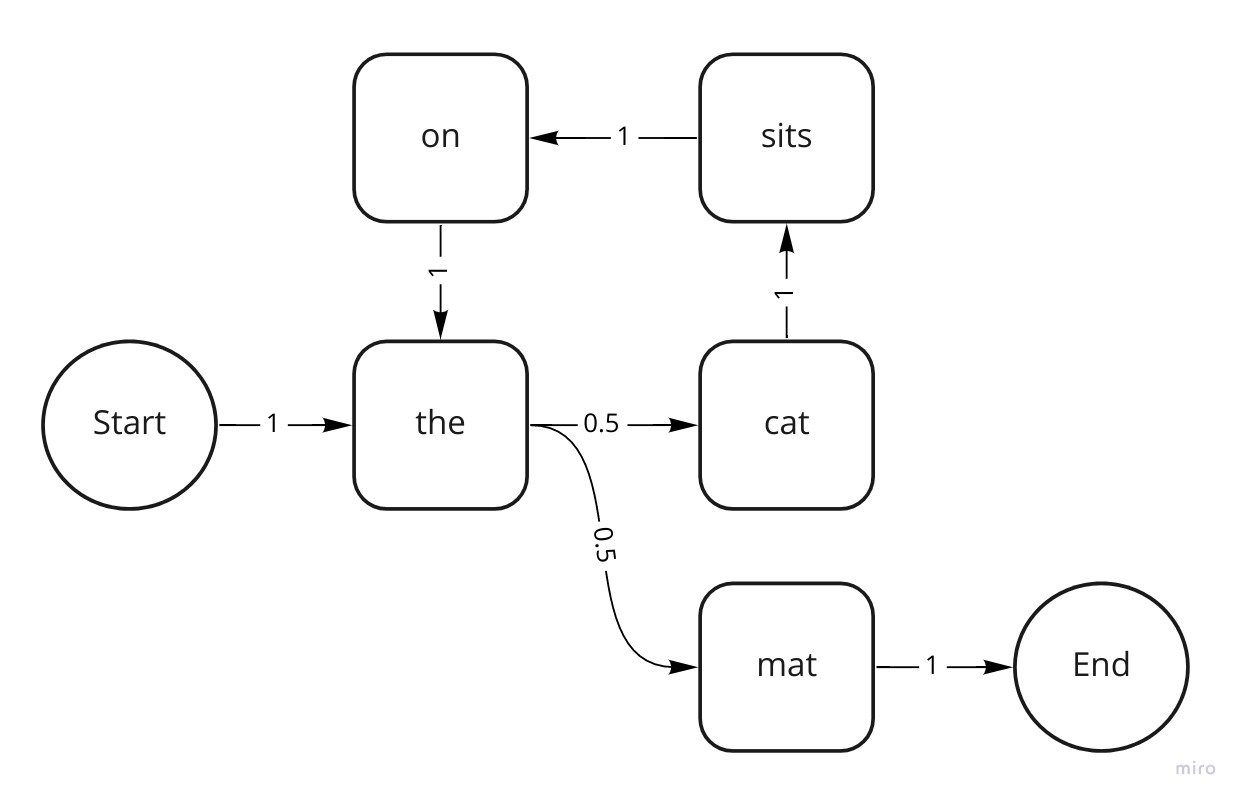
the cat sits on the mat

Learning

Learning is simply a matter of grouping and counting all transitions from each word to the next.

  def learn(learnSet: List[Plot]): MarkovChain = {
    // Create a list of all transitions from one Token to another, including doubles
    val tuples: List[(Token, Token)] = learnSet.flatMap { plot =>
      plot.sliding(2).toList.map { case List(from, to) => (from, to) }
    }
    val transitions: Map[Token, List[Token]] =
      tuples.groupBy(_._1).map { case (from, tuples) => (from, tuples.map(_._2)) }
    // Count how often transitions occur from Token X to Token Y for all X and Y
    val countedTransitions: Map[Token, Links] = transitions.map { case (from, toTokens: List[Token]) =>
      val tos = toTokens.groupBy(identity).map { case (toToken, allSimilar) => Link(toToken, allSimilar.size) }
      (from, Links(tos.toList))
    }
    MarkovChain(countedTransitions)
  }

Output probability

With this Markov chain we can calculate the probability to output a certain plot.

P("The mat") = P(StartToken -> Word("the")) * P(Word("the") -> Word("mat")) * P(Word("mat") -> EndToken)
             = 1 * 0.5 * 1
             = 0.5

P("The cat sits on the mat") = 0.5 * 0.5 = 0.25
P("The cat sits on the cat sits on the mat") = 0.5 * 0.5 * 0.5 = 0.125

P(all) = 0.5 + 0.25 + 0.125 ...... = 1

This is a rather simple Markov chain, which can only repeat "cat sits on the" in the middle a number of times.

If we add up all these (infinite) possibilities, we see that the total probability adds up to 1

This method calculates the probability to output a list of tokens.

  def probabilityToOutput(tokens: List[Token]): Double = tokens match {
    case List()         => 0.0
    case List(EndToken) => 1.0
    case head :: tail =>
      transitions
        .get(head)
        .orElse(transitions.get(InfrequentWord)) //if this token has not been learned on
        .map(_.probabilityToOutput(tail.head) * probabilityToOutput(tail))
        .getOrElse(0.0) //if it also has not learned InfrequentWord
  }

In the next part we’ll use this probability to make a classifier

shadow-left